几十年前,美国历史上最为(能)杰(撒)出(谎)的国务卿基辛格接受记者采访时曾被问及这样一个问题:“成绩出色的你为何没有选择留校任教?”基辛格给出了这样的回答:“学术圈的混乱情况使我向往中东地区关系的单纯。”虽有调侃的意味,却也道出了学术界派系争斗的残酷现实。而时下如火如荼的深度学习的发家史几乎可以说是这一情况最深刻的写照。为了能够全面的介绍Hinton及他宏大的Capsule计划,我们就有必要对深度学习(神经网络)的苦难发展史做一个简要的回顾。本文为第一部分,主要介绍早起情况及反向传播。
童年的悲惨世界--感知器
神经网络的理论根基出现的非常之早。1949年Hebb提出了大名鼎鼎的Hebb rule,随后在1957年Frank Rosenblatt基于这一理论设计出了感知器。从现代观点来看,这就是一个单层的最为简单的神经网络,同时其权值更新机制只靠单纯的叠加分类结果来实现。如此简单粗暴的方法自然不可能应对复杂的问题,对于非线性分类问题几乎可以说是无能为力。 在故事情节推进之前我们还需要简单的介绍一下故事背景,尽管学术圈中有一众大牛都是做人工智能的,但是这些大牛之间可没有什么阶级情感。因为人工智能领域立山头的情况非常严重,根据其理论基础主要分为四大派系:1、连接主义(来源:神经科学,代表理论:神经网络),2、符号主义(来源:逻辑学,代表理论:专家系统),3、进化主义(来源:遗传生物学,代表理论:遗传算法),4、贝叶斯派(来源:统计学,代表理论:贝叶斯网络)。正如中国的各个门派之间要打个你死我活一样,这些派系之间也是常年的你来我往。而当时人工智能最为推崇的大牛是符号主义的马文明斯基。如果我们以神经网络为第一主角写篇小说,那这位老斯基无疑会成为最大的反面boss。当时的进化主义和贝叶斯派发展的还非常稚嫩,所以自然不会获得明斯基的关注,而偏巧神经网络由于具备模仿人类神经系统的特点,很容易让人把它和正统的人工智能结合起来。看到此情此景老爷子坐不住了,本着趁它虚要它命的精神,老爷子写了一本书,叫做《感知器》。不过不要被书名骗了,马老爷子可不是学雷锋帮忙推广感知器,他写这本书的感觉就好像是乔布斯心血来潮写了本《伟大的微软》或者马化腾搞了本《崛起的360》一样:书中强调指出了感知器的在解决XOR等非线性问题的拟合上的局限性,再加上老爷子本身的巨大影响力,使得这一招直中要害,几乎打得神经网络10年没缓过神来。而Hinton正是在这个寒冰期攻读的神经网络的研究生,所以他曾在吴恩达的采访中追忆起当时的悲惨情景。有图为证:

这种感觉就好像是现在的你花了大价钱跑到蓝翔去学习BP机修理专业一样,在正常人眼里都是不可理喻的行为。 好在当时的美国还有对神经网络理论抱有兴趣的团队,最终接纳了Hinton。而事实也证明天道有轮回,Hinton的这一坚持也带来了回报,其不懈的努力终于换来了带来神经网络第一次复兴的技术--反向传播算法。
青年的文艺复兴--反向传播
正如罗杰彭罗斯在《皇帝的新脑》中曾经提到的一样,一本书中的每一个数学公式都会吓跑一半的读者,所以我这里尽量用概念性的描述来阐述反向传播的问题。不过,为了能够避免语言过于晦涩,还是会稍微涉及到一些小学数学公式及最简单的求导概念,如果你有困难的话可以来找我讨论。此外,对反向传播的语言阐述的简单和数学上实现其计算的困难会形成鲜明的对比。同组的老葛和我聊起这个事的时候还吐过槽:现在搞深度学习的,十个人里有九个不会写反向传播。玩笑归玩笑,其实我个人感觉这个比例甚至于还有点过于乐观了。 在开始正题之前,先要插播个广告。对于反向传播,目前看到所有的学术著作和网络短文及在线课程当中对其概念和原理阐述的最通俗易懂的当属Colah的博客Colah’s blog(这个Colah与Stanford的Andrew Kaparthy合称深度学习博客界的网红姐妹花,其对LSTM的介绍博客几乎被全天下的人引用)。为了尊重知识产权,这里只会简单的摘出其中的核心部分来讲述,如果想查看全文请点击原文链接。此外在征得了Colah大神本人的同意后我打算在另一篇博客将该文章全文汉化,一看英文就犯困的同学也可以考虑一下。 接下来我们首先介绍计算图的概念。
计算图
神经网络在进行计算的过程中并非是像普通意义上的数学一样公式化,本着一图胜千言的原则。很多深度学习库在处理神经网络的整个计算流程表示是通过图模型来实现的,而这个代表了整个计算流程的图,简称计算图,一个简单的栗子如下: 假如我们想要做如下的一组计算:
那么通过计算图来表示这个计算流程的效果如下:
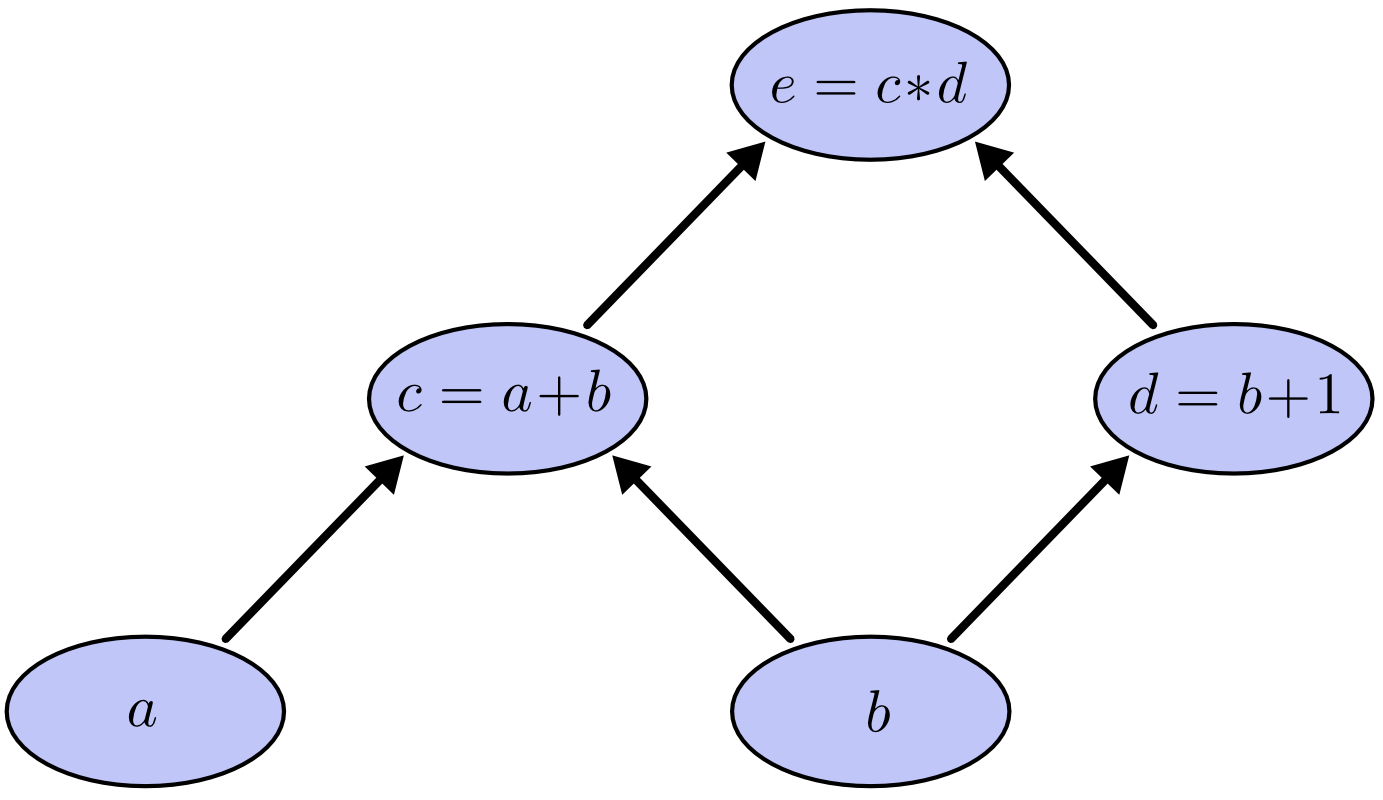
在计算图中,每个节点(node)代表一个变量及该变量的计算过程(算子),而连接节点的箭头代表了变量的输出方向,即哪些变量的计算需要该变量,比如指向c的a和b两个节点的箭头就代表了为了计算c必须获得a和b两个变量,这与我们刚才写出的\(c=a+b\)公式相对应。 构建好了计算图之后,我们就可以按照箭头流向进行计算了,计算过程中只需要记住一点:当指向一个node的所有node都已经求值后,就可以按照node中的算子对该node的值进行计算。在该计算图中,只需要按照顺序计算a,b->c->d->e即可,其中a,b为已知输入量。这里我们假设a,b分别为2和1,那么根据以上流程完成的计算图如下所示:
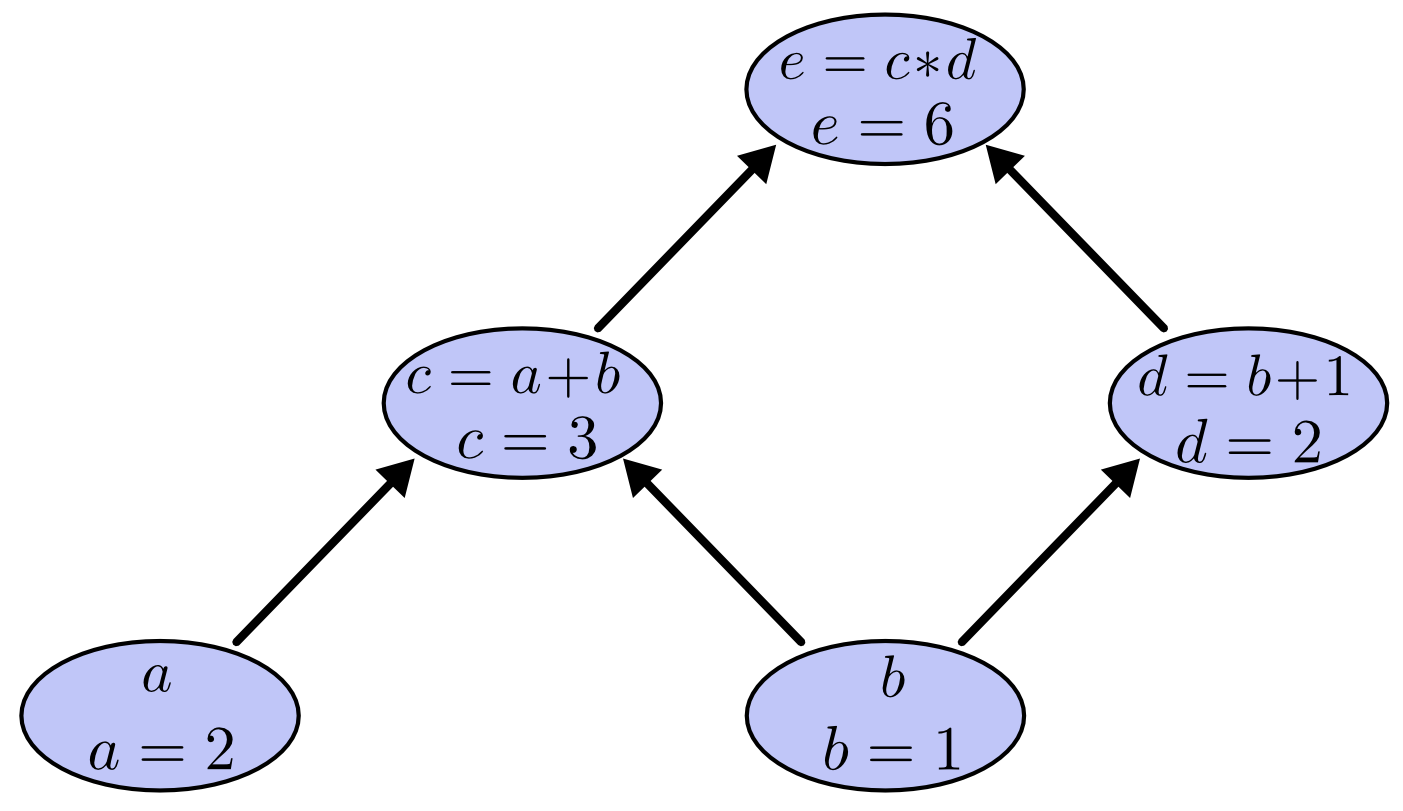
计算图的导数
在了解了计算图的基本概念之后,我们接下来分析各个元素相互之间的影响。从计算图可以看到,箭头起始的变量对箭头指向的变量是具有直接影响的,如a和b影响c,b直接影响d,那么a的变化会对c产生多大的影响呢?对这些变化的定量估计就需要用到本篇当中最难的一个数学概念了:偏导数。不过没有学过偏导也没关系,因为我们举的都是线性函数的例子,你只需要了解如下这个基本公式就好了: 某个变量a对b的偏导一般表示为 对于线性函数\(y=c_0x\)来说,我们有 而如果两个变量a和b不相关时,我们有
其偏导等于线性函数的参数。 对于我们的计算图,可以求出如下的结果: 类似的,对于e,我们有:
从整个计算图的角度来看,进行求导后的效果如下:
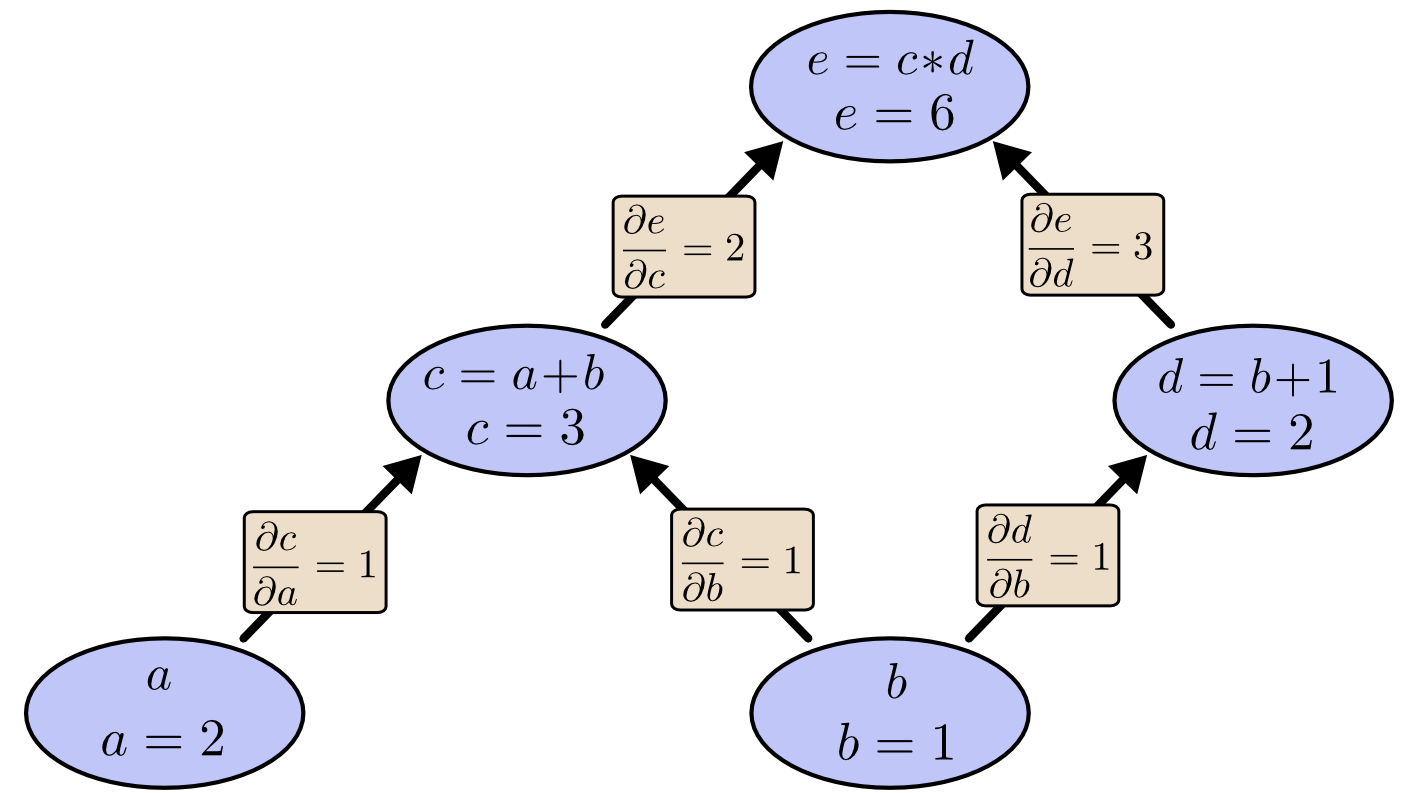
那么对于非直接连接的变量间的相互影响该如何估计?很简单,找到两个变量对应node的连接路径,将路径上的偏导乘个遍就可以了。例如在上图中如果我们想要计算\(\frac{\partial c}{\partial a}\)的话怎么办,只要沿从a到c的路径把所有偏导值都乘起来就ok。计算过程如下:
So easy, huh? 但是如果我们要求的是\(\frac{\partial e}{\partial b}\)呢?这个时候我们就面临问题了,因为从b到e有两条路径,而这个偏导的正解是把两路的乘积相加,也就是:
这也就完成了偏导的求解。当然,如果认为仅仅这样就能搞定所有的神经网络就太naive了。在这个说明范例中我们最多只有两路路径,而在实际应用中,在不同节点之间的通路可能成百上千,如果还采用这种原始的暴力计数方法很明显是有悖科学精神的,所以我们来探索一下多路情况下该如何计算这些node之间的相关性?
因子路径
下面我们来考虑一个更加一般化的问题,如果不同节点间存在几个通路,该如何给出一般化的解法?下面我们先来实现一次智商上的巨大飞跃,将通路数量从2条增加至3条~。具体的通路图像如下图所示:
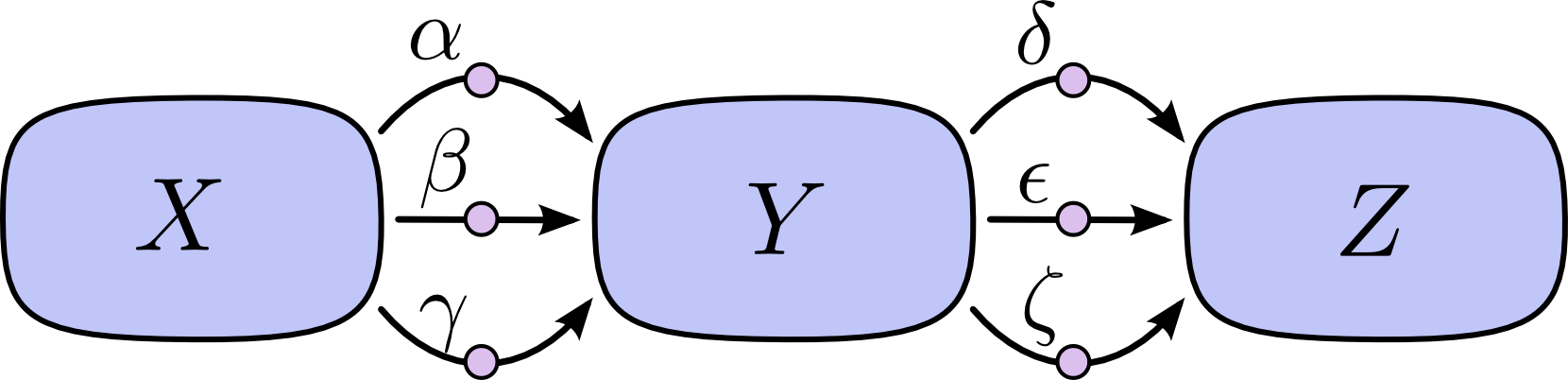
那么\(\frac{\partial Z}{\partial X}\)的值是多少呢,评着过硬的数数本领,我们可以查出答案应该是:
只有9个项,所以我们的手指头基本还够用,但是如果我们把支路都变成5的话答案就是25项,这时候就算是手脚并用也解决不了这个问题了。 当然,学过因式分解的小朋友可能已经发现了更简洁的表示方式:
基于这种方式,答案的项数就能够得到大大的简化,我们也不用再去笨拙地一条条地去数路了,但是后边这种表示方式是通过数学求解获得的,其是否具有计算图的解释呢?答案是有的:
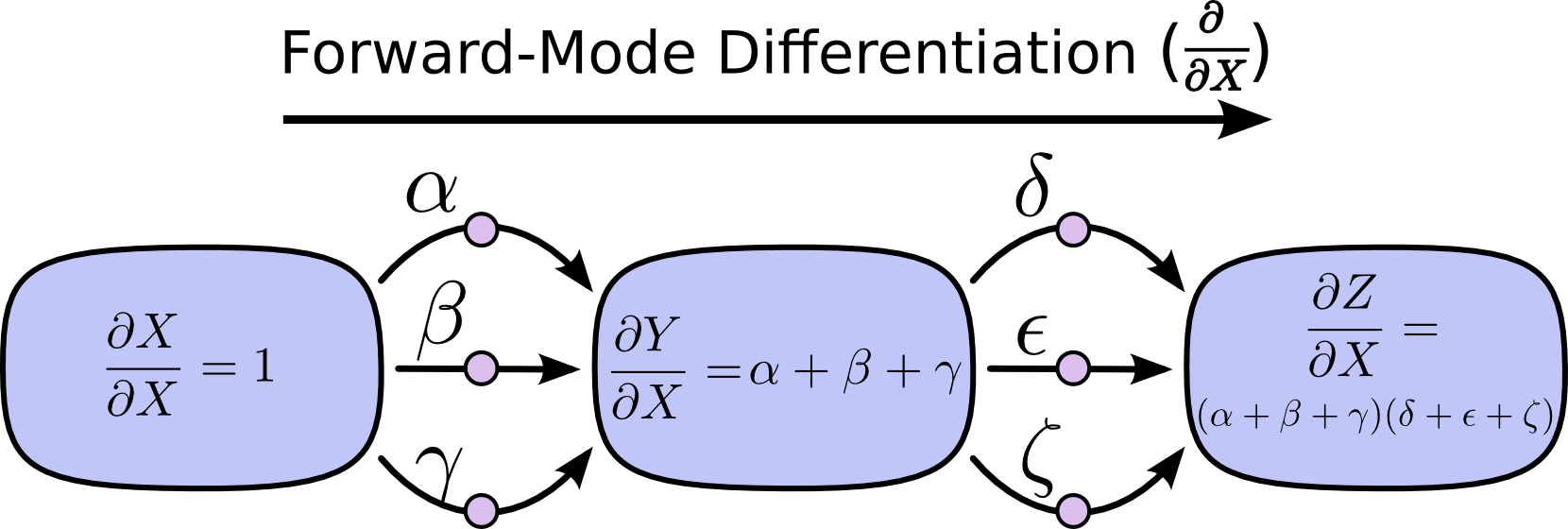
如果对每个节点我们都对X求导,就能得到所有节点和X变化之间的相互关系,也就如上图所示,而对这些关系采用连锁乘法就得到了最终解。 当然,我们还可以开开脑洞,看看所有节点的变化和Z之间的关系,然后就能得到下图:

殊途同归,最终得到的\(\frac{\partial Z}{\partial X}\)是完全相同的,而这种思路,学名就叫做反向传播。
重回主题
在这些图之间前向后向的绕了半天以后,我们重新回归主题,最开始给出的图,对应前向和反向应该如何计算? 首先我们看前向的求解,现在我们求解所有node关于b到导数
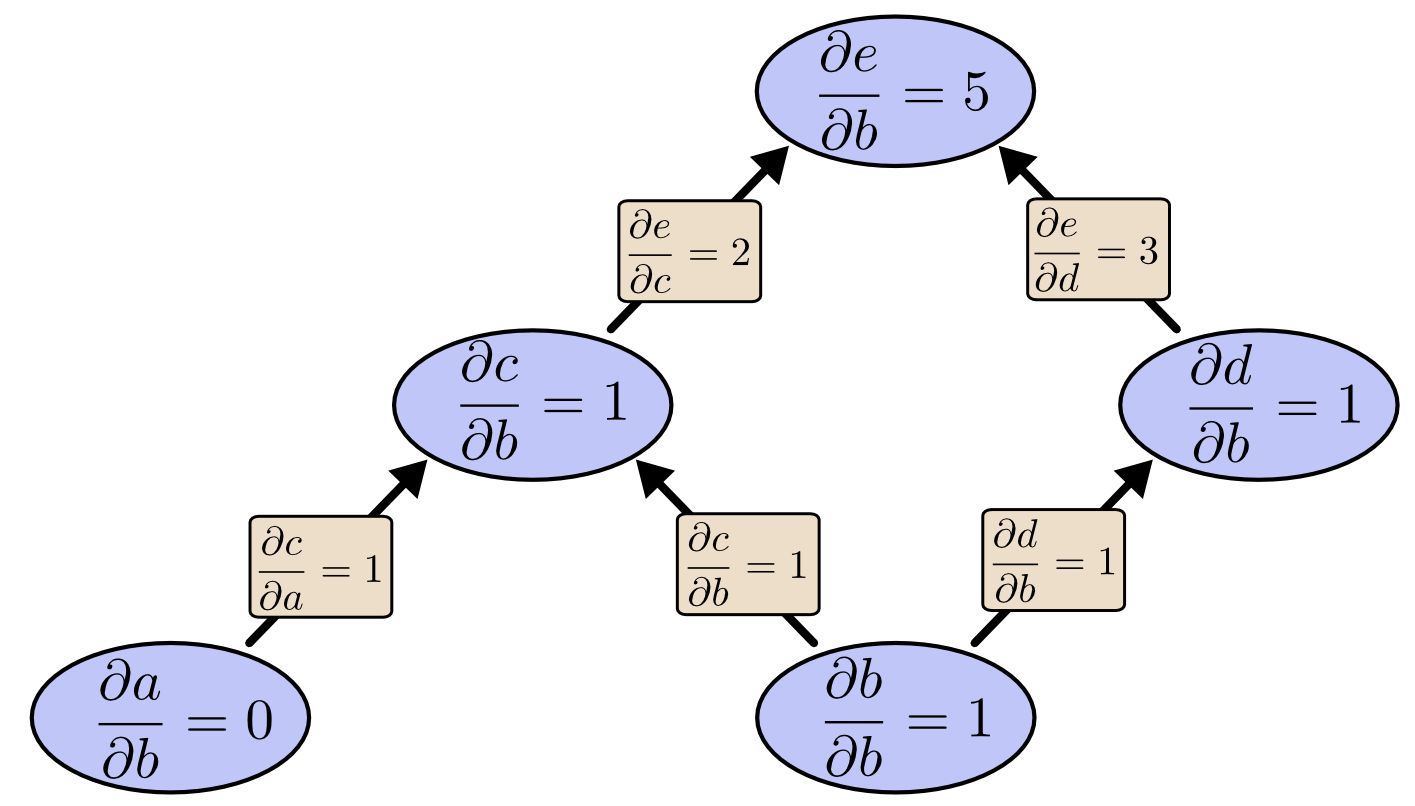
还是so easy, 可惜的一次计算是不够的,如果我们还想知道\(\frac{\partial e}{\partial a}\),我们还要从头来过再计算一遍。而反向传播的表现如何呢?
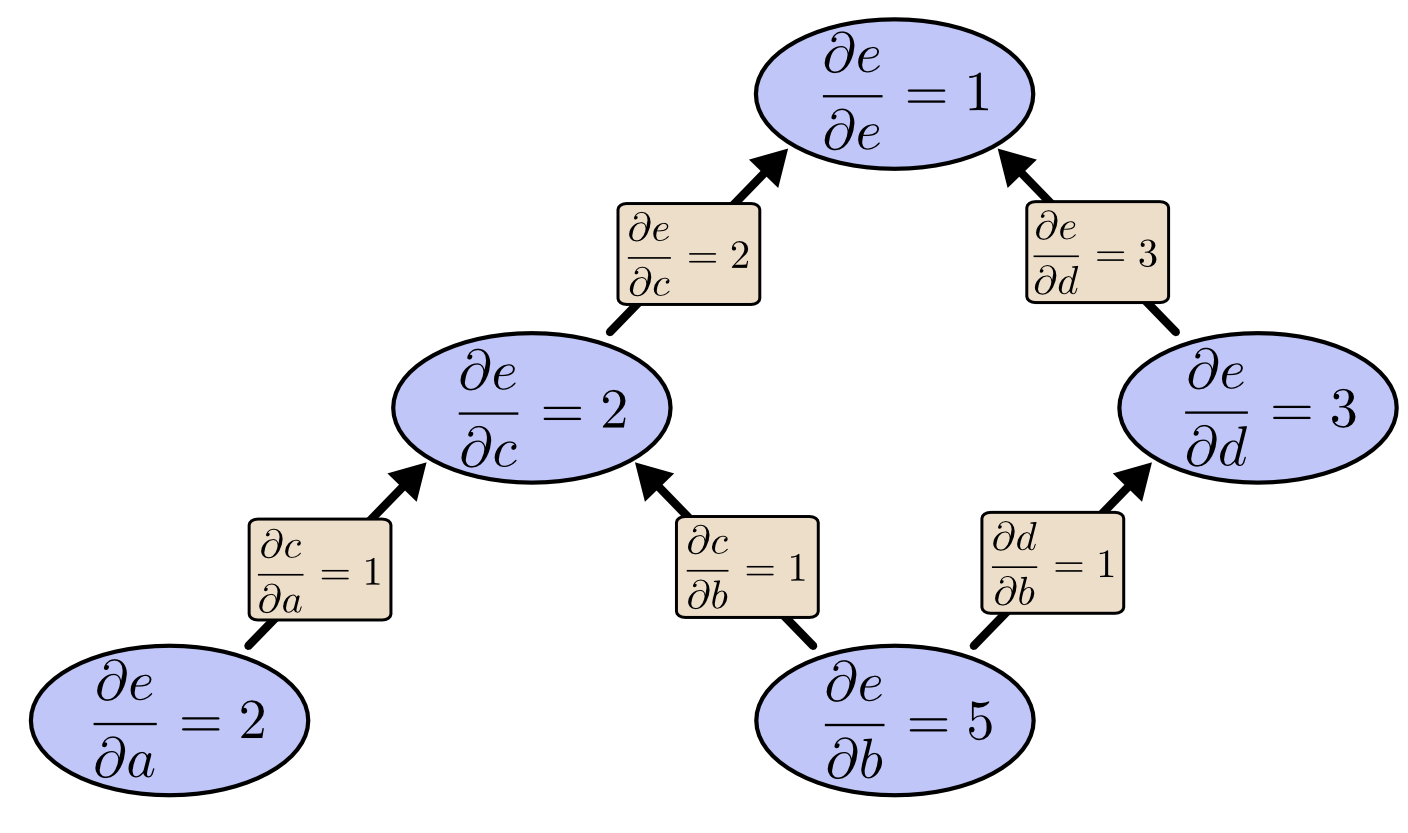
我们会发现我们感兴趣的\(\frac{\partial e}{\partial a}\)和\(\frac{\partial e}{\partial b}\)同时被求出了。惊不惊喜?意不意外?这就是反向传播的魅力,这还仅仅是两个输入,通常情况下我们的输入会有成千上万,这种情况下采取不同的梯度计算顺序就会带来上万倍的效率差别。这也是反向传播的魅力所在。
总结和预告片
反向传播的算法核心思想并不复杂,然而它却为多层神经网络的训练指明了方向。当然,反向传播实际的理论推倒和表达要晦涩很多(你不能指望Hinton用几个单变量的例子配合几幅漂亮的图片就能带动起神经网络的文艺复兴,毕竟其他流派的大牛们也不是吃素的)。为了尽量不吓跑读者,我尽量删除了这些晦涩的公式,感兴趣的朋友可以自行查阅。
反向传播的出现带来了多层神经网络的繁荣,但是在发展的过程中,由于其存在固有的缺点,在实际应用中无法得到有效地普及和使用。从而导致其发展出现了新的低谷。当然在这一过程中,免不了要提及Hinton和贝叶斯派代表人物Michael. I. Jordan(请不要与打球的那个混淆)之间的爱恨情仇,以及神经网络与概率图的相爱相杀的故事。在这神经网络低谷时期,Hinton开始尝试从物理系统而非神经系统获得一些启示。下期的理论核心就是Hinton在贝叶斯派大行其道这一阶段所做的一些地下工作--玻尔兹曼机。下期再会!